Estimating Pi using Quantum Computer

Approximating pi has roots in QFT and QPE, a good application for both the concepts.

Resources used : https://www.youtube.com/watch?v=5kcoaanYyZw&t=622s; and https://www.youtube.com/watch?v=YpcT8u2a2jcm

The basic step by step process

estimating_pi.png

import math
from qiskit import QuantumCircuit
from qiskit import Aer, execute
from qiskit.visualization import plot_histogram

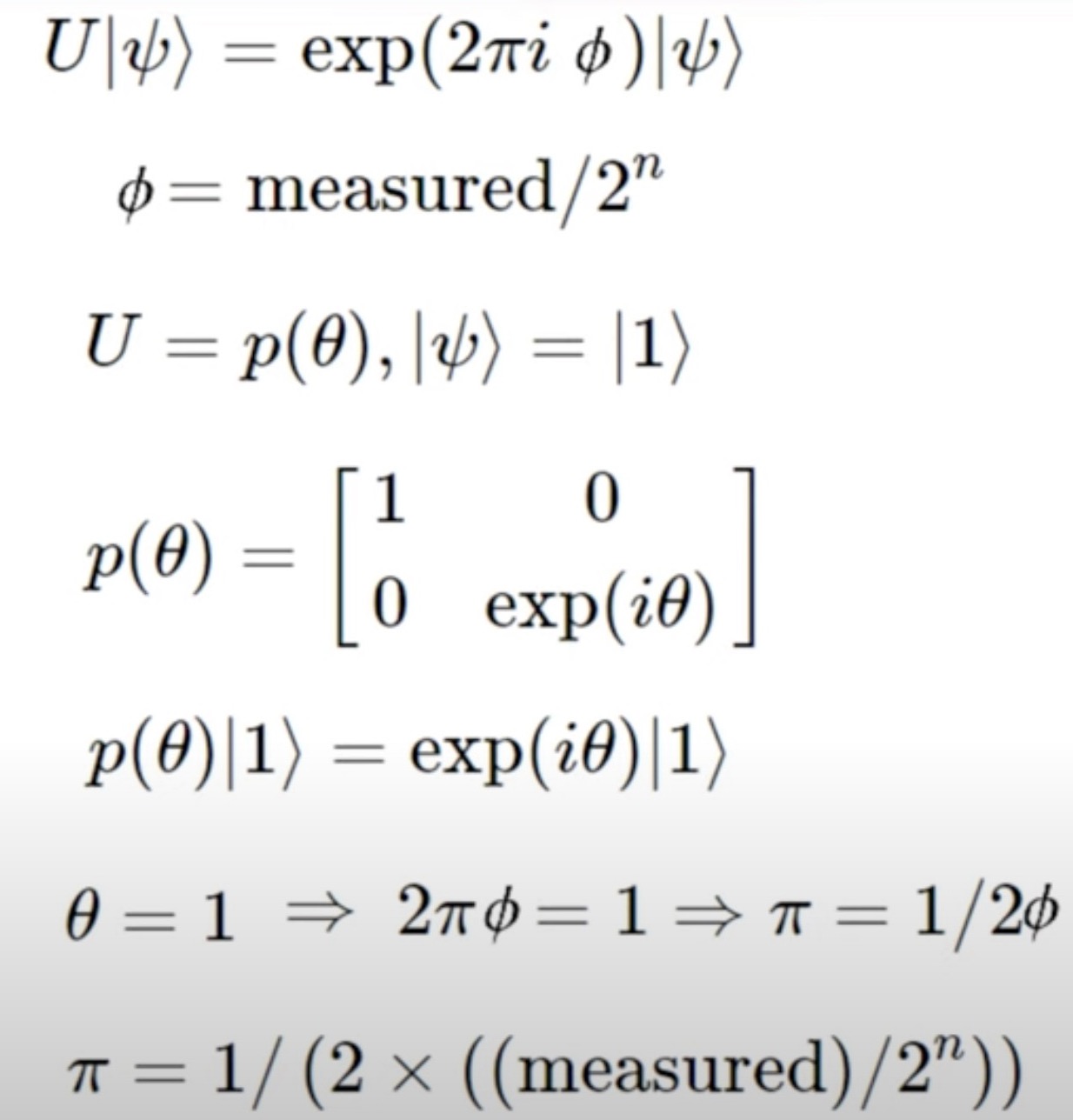
Build the first part of QPE before the Inverse QFT, it involves a series of Hadamard and Unitary

n = 4
circuit = QuantumCircuit(n + 1, n)

def qpe_initial(circuit, n):
    circuit.h(range(n))
    circuit.x(n)

    for x in reversed(range(n)):
        for a in range(2**(n-1-x)):
            circuit.cp(1, n-1-x, n)
    return circuit

test = qpe_initial(circuit, n)
test.draw('mpl')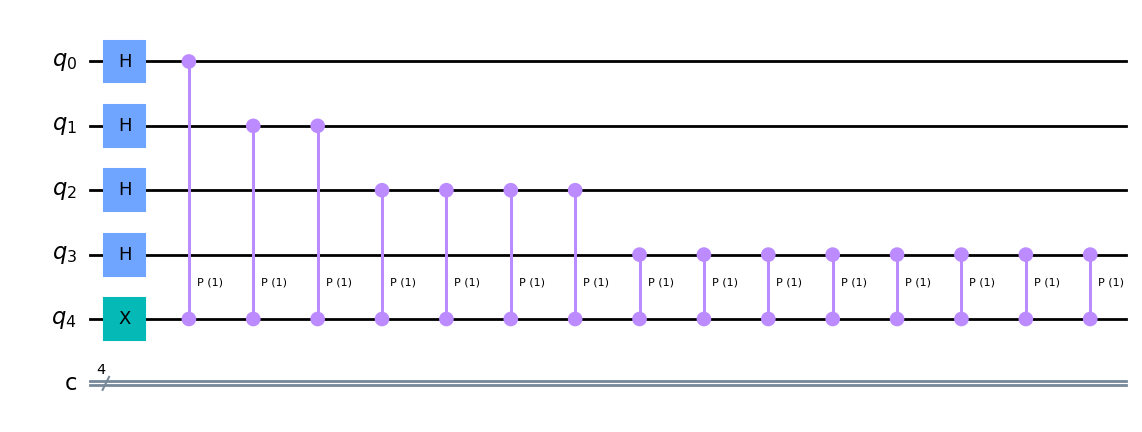

Inverse QFT

def iqft(circuit, n):
    for q in range(int(n/2)):
        circuit.swap(q, n-q-1)
    for j in range(0,n):
        for m in range(j):
            circuit.cp(-math.pi/float(2**(j-m)), m, j)
        circuit.h(j)
    return circuit

test = iqft(test, n)
test.draw('mpl')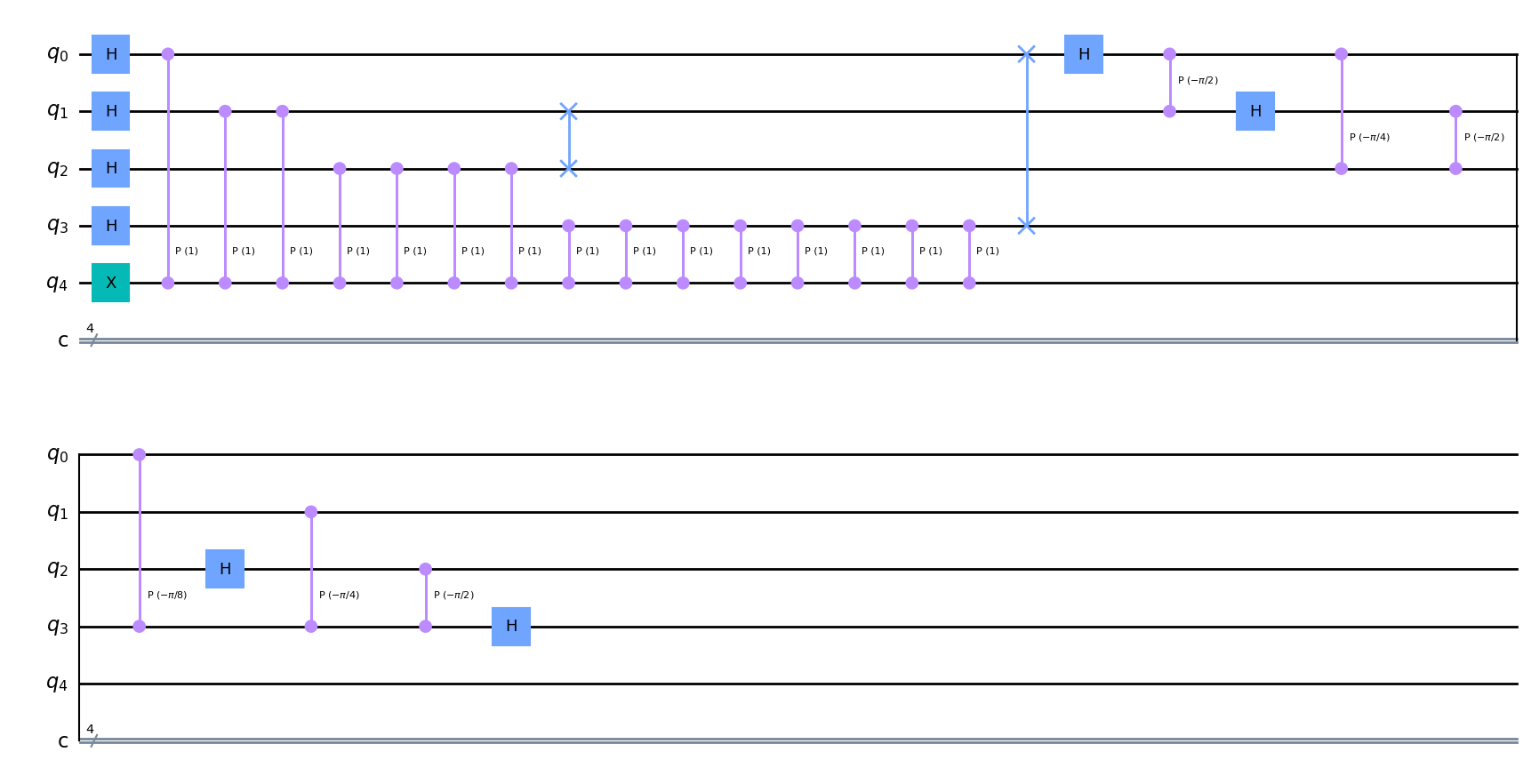

test.measure(range(n), range(n))

<qiskit.circuit.instructionset.InstructionSet at 0x7fbdab490e20>

test.draw('mpl')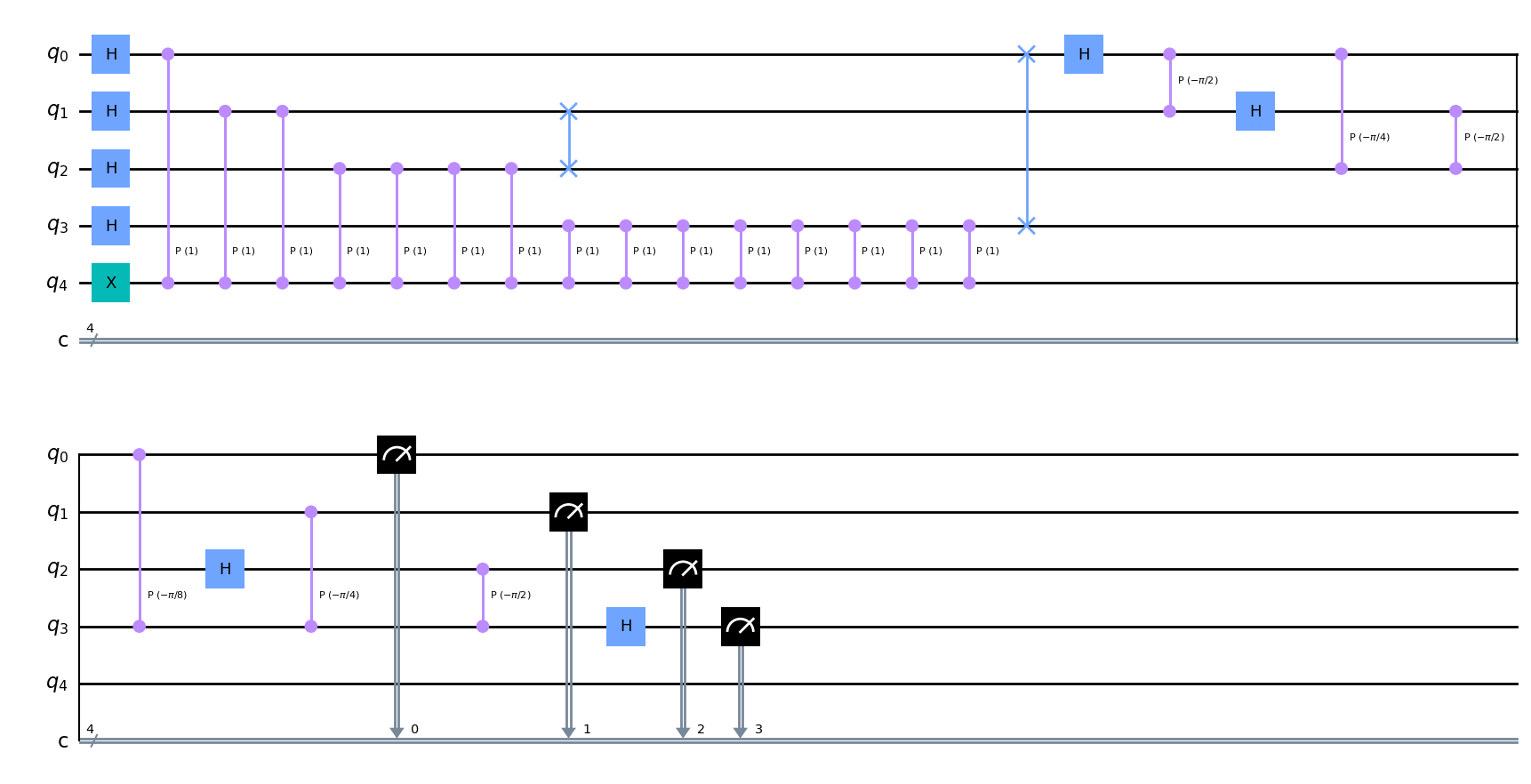

simulator = Aer.get_backend('qasm_simulator')
counts = execute(test, backend=simulator, shots=10000).result().get_counts()

counts

{'1011': 46,
 '1001': 44,
 '0101': 166,
 '1110': 71,
 '0000': 175,
 '1111': 93,
 '1101': 50,
 '1010': 45,
 '1000': 39,
 '0100': 478,
 '1100': 58,
 '0111': 63,
 '0011': 4926,
 '0001': 453,
 '0110': 102,
 '0010': 3191}

max_counts_result = max(counts, key=counts.get)
max_counts_result

'0011'

max_counts_result = int(max_counts_result, 2)
max_counts_result

3

theta = max_counts_result/2**n
val = 1./(2*theta)
val

2.6666666666666665

This seems ok, putting it all together

def estimate_pi(n):
    print("estimating for qubit", n)
    circuit = QuantumCircuit(n + 1, n)
    circuit = qpe_initial(circuit, n)
    circuit = iqft(circuit, n)
    circuit.measure(range(n), range(n))
    counts = execute(circuit, backend=simulator, shots=10000).result().get_counts()
    max_counts_result = max(counts, key=counts.get)
    max_counts_result = int(max_counts_result, 2)
    theta = max_counts_result/2**n
    val = 1/(2*theta)
    return val

Kernel dies on 14th iteration, so restrict number of qubits to 14

pi_values = []
range_n = 14
for i in range(2, range_n):
    pi_values.append(estimate_pi(i))

estimating for qubit 2
estimating for qubit 3
estimating for qubit 4
estimating for qubit 5
estimating for qubit 6
estimating for qubit 7
estimating for qubit 8
estimating for qubit 9
estimating for qubit 10
estimating for qubit 11
estimating for qubit 12
estimating for qubit 13

pi_values

[2.0,
 4.0,
 2.6666666666666665,
 3.2,
 3.2,
 3.2,
 3.1219512195121952,
 3.1604938271604937,
 3.1411042944785277,
 3.1411042944785277,
 3.1411042944785277,
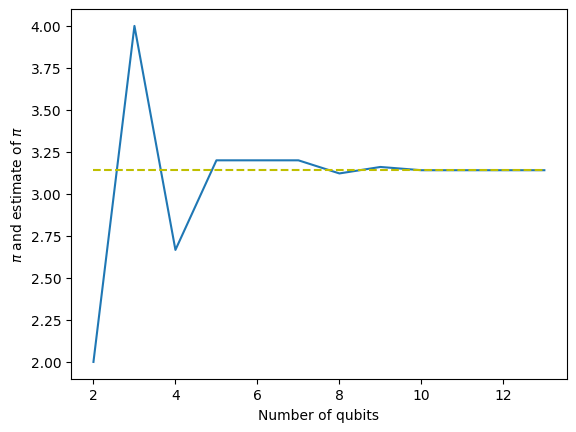
 3.1411042944785277]

Plot

import matplotlib.pyplot as plt

plt.plot(list(range(2,14)), pi_values)
plt.plot(list(range(2,14)), [math.pi]*len(list(range(2,14))), '--y')
plt.xlabel('Number of qubits', fontdict={'size':10})
plt.ylabel('$\pi$ and estimate of $\pi$', fontdict={'size':10})

Text(0, 0.5, '$\\pi$ and estimate of $\\pi$')